Il n’est pas facile de se procurer de la poudre de lycopode, mais si vous avez la chance d’en avoir quelques grammes à votre disposition, voici une expérience qui vous illustrera la nature ondulatoire de la lumière.
La figure de diffraction d’une lumière monochromatique et la décomposition de la lumière blanche par de la poudre de lycopode montrent qu’il n’y a pas formation d’ombres géométriques derrière des objets très petits.
Fiche d’accompagnement de l’expérience:
 Matériel
Matériel- un pointeur laser vert (532 nm)
- des lames porte-objet de microscope ou bien des cadres de diapositives avec verre
- de la poudre de lycopode
- un corps gras visqueux, par exemple de la crème pour la peau, du beurre ou de la graisse
- un écran sur pied
- éventuellement une bougie
- des supports et pinces
 Montage et réalisation
Montage et réalisationPlacer à 50 cm d’un écran une plaque de verre légèrement grasse sur laquelle de la poudre de lycopode a été saupoudrée.
Orienter un faisceau laser vert pour qu’il éclaire cette plaque perpendiculairement.
Observer sur l’écran la figure de diffraction obtenue et présentant une tache éclairée au centre entourée par des anneaux concentriques alternativement sombres et clairs.

On peut également regarder une source de lumière blanche (par exemple la flamme d’une bougie allumée située à grande distance) à travers la plaque portant la poudre de lycopode, on voit alors les différentes couleurs du spectre former des cercles concentriques autour de la source de lumière.
 Explications
ExplicationsLorsque de la lumière cohérente arrive sur la poudre de lycopode, chaque grain se comporte comme un centre de diffraction qui crée une figure de diffraction sur l’écran.
Si le faisceau de lumière est étroit et parallèle et si les grains ont pratiquement la même taille (ce que nous constatons ici) alors les figures de diffraction des différents grains sont identiques et très peu décalées les unes par rapport aux autres.
Leur superposition sur l’écran forme une figure de diffraction unique identique aux figures de diffraction individuelles mais plus intense.
Vous disposez d’une règle pour mesurer le diamètre des anneaux de diffraction.
En dehors de la zone centrale qui correspond à la section du faisceau laser, la figure de diffraction obtenue est identique à celle qu’on observe lors de la diffraction par un trou de diamètre égal à celui d’un grain de lycopode. Ceci est conforme au théorème de Babinet qui affirme que la figure de diffraction d’un obstacle plan de forme quelconque est identique à celle qu’on obtient avec un trou de même forme percé dans un matériau opaque et situé au même endroit. En fait ceci est valable sauf dans la direction du faisceau incident.
La position des maxima de lumière sur la figure de diffraction dépend de la longueur d’onde. C’est la raison pour laquelle la lumière blanche est décomposée et ses différentes composantes sont vues dans des directions d’inclinaisons différentes par rapport à l’axe optique.
Essayez de déduire la taille des grains de poudre de lycopode.
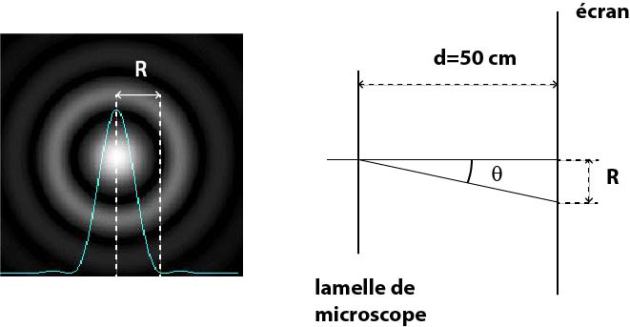
L’angle 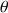 du premier anneau sombre de la tache d’Airy est donné par :
du premier anneau sombre de la tache d’Airy est donné par :
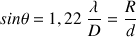
où 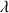 est la longueur d’onde de la lumière diffractée et D le diamètre de l’objet diffractant.
est la longueur d’onde de la lumière diffractée et D le diamètre de l’objet diffractant.
Nous pouvons alors calculer le diamètre D de l’objet diffractant :
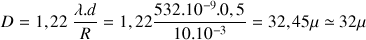
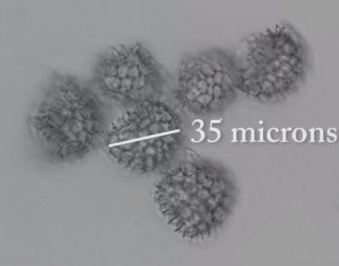
Nous pouvons vérifier ce calcul grâce au microscope électronique qui nous permet de l’estimer à environ 35 microns.
 Remarques
RemarquesLorsqu’il y a de fines gouttelettes d’eau de taille identique dans l’atmosphère, on observe des anneaux colorés autour de la lune : ils constituent une figure appelée « halo ».
 Références
RéférencesDiffraction par une ouverture circulaire UEL

